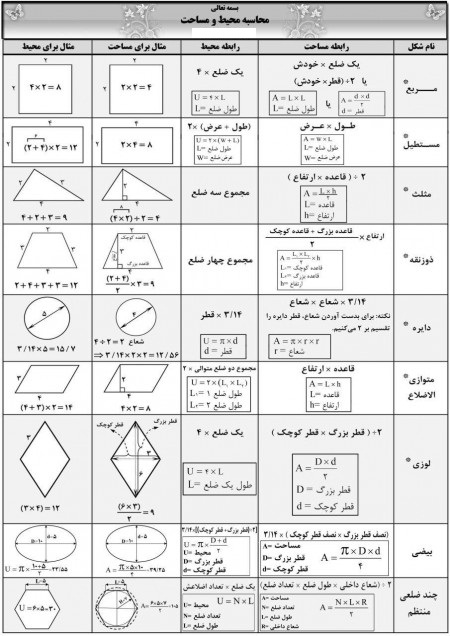
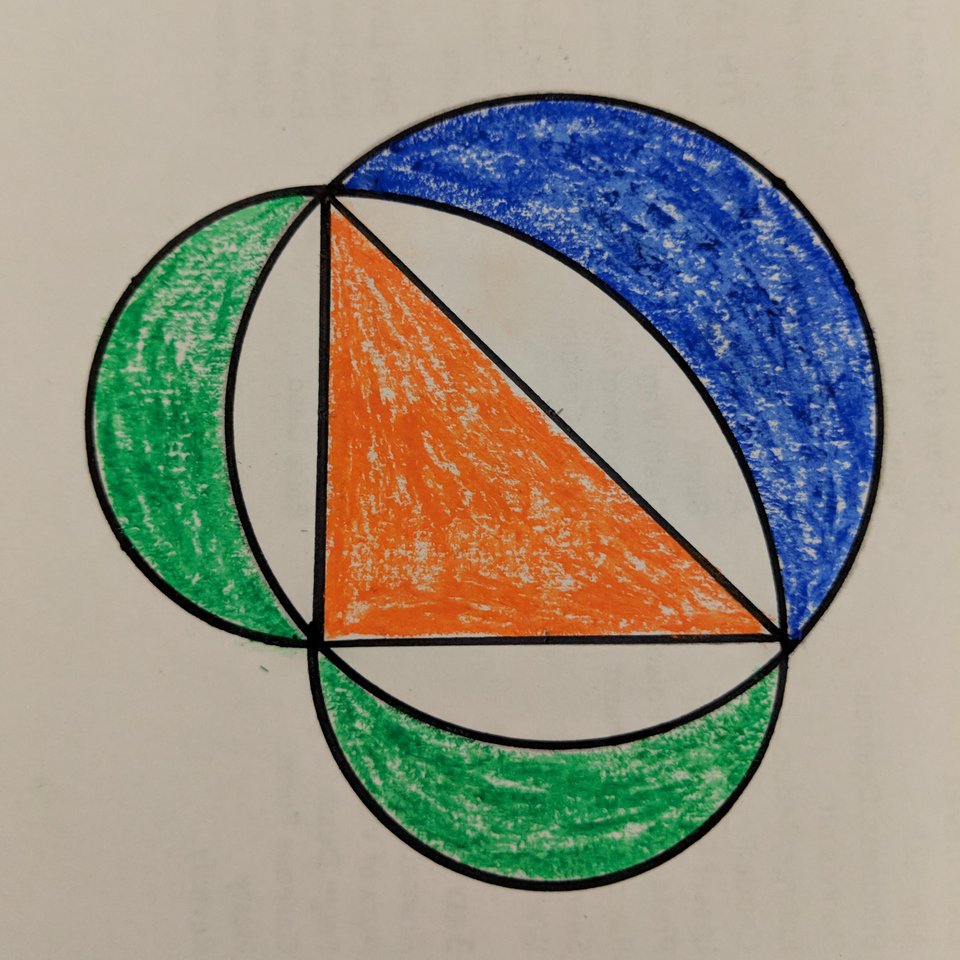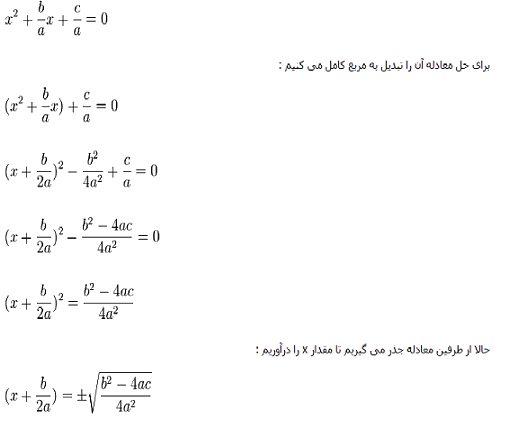هلالین بقراط

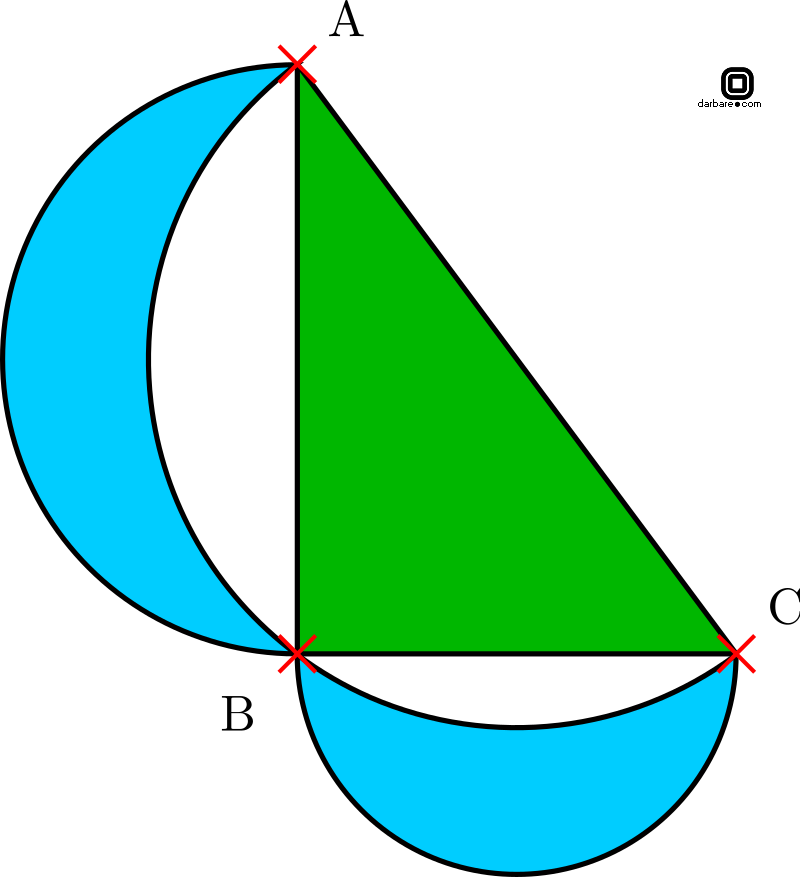
اگر از 3 ضلع مثلث قایم الزاویه ای 3 نیم دایره بکشیم آنگاه هلال هایی که در ضلع های قایمه بوجود آمد را هلالین بقراط.

هلالین بقراط. هلالین بقراط در شکل زیر مثلث abc قائم الزاویه و نیم دایره ها به قطر اضلاع مثلث رسم شده اند ثابت کنید مساحت قسمت سایه خورده با مسحت مثلث برابر است. مثلثات ویرایش نوشتار اصلی. یمیرکراجنیلع هدنسیون یپلاکیدار یزاجم تاراشتنا ادخ مان هب هسدنه و تایضایر رد اه للاه هریاد د زا نامک د نیب رصحم حطس للاه تسا تایضایر لاکشا زا یکی للاه. اینجا را کلیک کنید.

هلال بقراط در واقع بخشی از تحقیقات بزرگتری بوده است تحت عنوان تربیع دایره به این معنی که بتوان مربعی ساخت که مساحتش برابر دایره داده شده باشد. هلالین بقراط یک مسئله بسیار معروف و قدیمی هندسه است که در راه حل آن از قضیه فیثاغورس استفاده می شود. هلال بقراط به سطح هاشور خورده در بالا سمت چپ اطلاق می شود که مساحتی معادل مثلث هاشور خورده پایینی دارد. همتون بقراط رو میشناسید یکی از کشفیاتش همین هلالین است.

اگر در مثلث قائم الزاویه مستطیل مربع و یا نیم دایره تشکیل دهیم مساحت شکلی که بر روی وتر ساخته می شود برابر مجموع مساحت. هلالین بقراط این مسئله از بقراط ریاضی دان یونانی است و به هلالین بقراط مشهور است. مجموع مساحت های هلالین بقراط با مساحت مثلث قائم الزاویه برابر است.